Conjuntos Numericos

Los conjuntos numéricos son agrupaciones de números que guardan una serie de propiedades estructurales.

Clasificación de números Complejos ℂ Reales ℝ Racionales ℚ Enteros ℤ Naturales ℕ 1: uno Naturales primos Naturales compuestos 0: Cero Enteros negativos Fraccionarios Fracción propia Fracción impropia Irracionales Irracionales algebraicos Trascendentes Imaginarios

Numeros Naturales

En matemáticas, un número natural (designado por ℕ) es cualquiera de los números que se usan para contar los elementos de un conjunto.

Es todo número perteneciente a la serie ℕ = {0, 1, 2, 3, 4, …} formada por todos los números que, a partir del cero (o ausencia de elemento), el uno inicia y sin término medio.

Puesto que los números naturales se utilizan para contar elementos, el cero puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del área de la ciencia, el conjunto de los números naturales puede presentarse entonces de dos maneras distintas:

         

Definición sin el cero: ℕ = {1, 2, 3 ,4, ...} Definición con el cero: ℕ = {0, 1, 2, 3, 4, ...}

un ejemplo claro de como utilizar los números naturales:

Los números naturales pueden usarse para contar (una manzana, dos manzanas, tres manzanas, …).

Números Enteros

Los números enteros (designados por ) son un conjunto de números que incluye a los números naturales distintos de cero (1, 2, 3, ...), los negativos de los números naturales (..., −3, −2, −1) y al 0. Los enteros negativos, como −1 o −3 (se leen «menos uno», «menos tres», etc.), son menores que todos los enteros positivos (1, 2, ...) y que el cero. Para resaltar la diferencia entre positivos y negativos, a veces también se escribe un signo «más» delante de los positivos: +1, +5, etc. Cuando no se le escribe signo al número se asume que es positivo. El conjunto de todos los números enteros se representa por la letra ℤ = {..., −3, −2, −1, 0, +1, +2, +3, ...}

Los números enteros no tienen parte decimal: −783 y 154 son números enteros, mientras que 45,23 y −34/95 no. Al igual que los números naturales, los números enteros pueden sumarse, restarse, multiplicarse y dividirse, de forma similar a los primeros. Sin embargo, en el caso de los enteros es necesario calcular también el signo del resultado.

Los números enteros extienden la utilidad de los números naturales para contar cosas. Pueden utilizarse para contabilizar pérdidas

ejemplos:

1. si en un colegio entran 80 alumnos nuevos de primer curso un cierto año, pero hay 100 alumnos de último curso que pasaron a educación secundaria, en total habrá 100 − 80 = 20 alumnos menos; pero también puede decirse que dicho número ha aumentado en 80 − 100 = −20 alumnos.

para el segundo ejemplo debemos dar clic en el siguiente enlace:

http://www.voki.com/pickup.php?scid=11489687&height=267&width=200

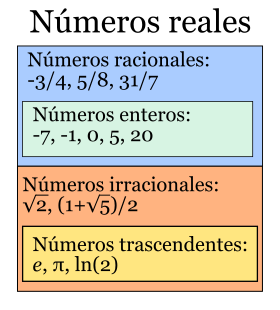
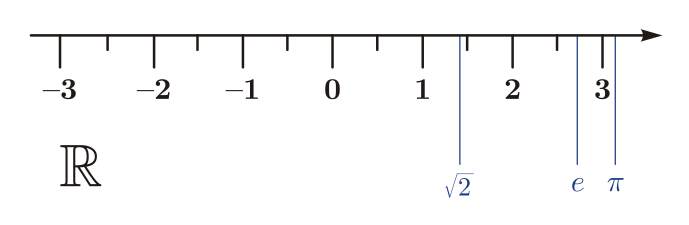
Numeros Reales

En matemáticas, los números reales (designados por ℝ) incluyen tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes

ejemplo:

 (1970) no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como: √5, π,

para mejor comprension les dejo estas imagenes:

Números Racionales

Número racional es todo número que puede representarse como el cociente de dos números enteros o, más precisamente, un entero y un natural positivo,¹ es decir, una fracción común  con numerador  y denominador  distinto de cero. El término «racional» alude a una fracción o parte de un todo. El conjunto de los números racionales se denota por Q (o bien , en negrita de pizarra).Este conjunto de números incluye a los números enteros (), y es un subconjunto de los números reales ().

En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada; de todas ellas, se toma como representante canónico de dicho número racional a la fracción irreducible. Las fracciones equivalentes entre sí –número racional– son una clase de equivalencia, resultado de la aplicación de una relación de equivalencia sobre .

La escritura decimal de un número racional es, o bien un número decimal finito, o bien periódico

Dos o más fracciones son equivalentes cuando representan la misma cantidad, y se escriben distinto.

• Ejemplo:

las fracciones , ,  y 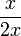 son equivalentes, ya que representan la cantidad «un medio».}

Numeros irracionales

En matemáticas, un número irracional es un número que no puede ser expresado como una fracción , donde  y  son enteros y  es diferente de cero. Es cualquier número real que no es racional.

No existe una notación universal para indicarlos, como , que es generalmente aceptada. Las razones son que el conjunto de Números Irracionales no constituyen alguna estructura algebraica, 

el numero irracional es un numero decimal que sigue para siempre y no se repite.

Ejemplo: Pi es un número irracional. El valor de Pi es

3,1415926535897932384626433832795 (y más...)